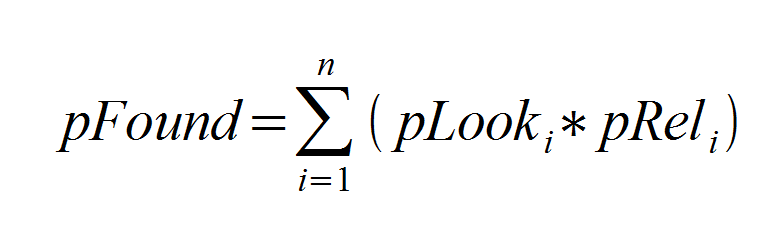Фундаментальные особенности MatrixNet
После нашей беседы о фундаментальных особенностях MatrixNet я получил несколько острых наводящих вопросов, ответов на которые очевидно не хватало в моём рассказе. Выражаю авторам вопросов свою благодарность:
Постановка проблемы
Итак, постановка вопросов для нашего совместного обсуждения:
Вопрос из личного опыта: почему удаётся вывести в топ по довольно конкурентным запросам сайты с помощью ссылок, которые обычно оптимизаторами считаются мусорными?
Вопрос из наблюдения за выдачей: только ли за счёт поведенческих факторов держатся в топе сайты без заметного невооруженным глазом массива ссылок?
Свежий вопрос, поставленный перед оптимизаторами Яндексом: почему в топе с 23 февраля (не с 12 марта !!!) 2014 года по запросам например, юридической тематики, в топ попали молодые сайты практически без ссылок и без какого-либо заметного трафика до и надолго ли они там?
Или другими словами это баги (ошибки) или фичи (особенности) MatrixNet?
Эти все вопросы можно свести к одному единственному: почему не падает pFound при отказе от использования ссылочных факторов в функции ранжирования или при отсутствии у документов поведенческих факторов?
Через тернии к звёздам
Ответ на этот вопрос очень простой, но подбираюсь я к ответу на него достаточно сложно, буквально через тернии к звёздам и в онлайн рассказе я сделал это крайне плохо. Попытаюсь исправится после дополнительной подготовки. И ещё раз всем спасибо за уточняющие вопросы.
Раскрывать особенности MatrixNet я буду при помощи особенностей алгоритмов определения параметров орбиты небесного тела по короткой дуге наблюдений. Во-первых потому, что мозг человека устроен так, что он пытается объяснить что-то новое при помощи хорошо известного старого. И определение орбит мне известно более-менее хорошо. А, во-вторых, потому, что метод выбора ранжирующей функции с помощью MatrixNet математически подобен методам определения орбит. С точки зрения математики разницы между методами нет никакой и MatrixNet можно обучить определять орбиты. А так же известно, что MatrixNet используется в геологоразведке. Это возможно потому, что все эти задачи математически подобны.
Доказательство подобия методов
Итак, как устроен внутри метод определения орбит? В 1801 году Карл Гаусс вместо строгого аналитического метода вычисления орбиты только что открытой первой малой планеты Цереры предложил свой собственный метод. Он разделил массив наблюдений на 2 части. По трём наблюдениям (положениям небесного тела) он построил семейство орбит, а с помощью остальных наблюдений он отобрал лучшую из орбит, то есть ту орбиту, которая дала минимальную сумму квадратов невязок. Этот метод именуется методом наименьших квадратов (мнк).

Невязка — это разность между наблюдённым значением O некой величины и вычисленным значением этой же величины C.
Но MatrixNet, и вообще многие методы машинного обучения, устроены подобным же образом. Массив «наблюдений», а в случае MatrixNet это оценки релевантности для пар <запрос, документ> разбивают на две части: обучающую и контрольную. Дальше каким-то способом строят семейство функций решений. Сам способ получения этого семейства как в случае Гусса так и в случае инженеров Яндекса является очень сильным know-how, но для нашей беседы этот способ не представляет ни малейшего интереса – это предмет для отдельного разговора.
Заключительный этап машинного обучения – выбор решения, то есть одной функции из семейства, дающего наилучшую аппроксимацию (то есть приближение) на контрольном множестве «наблюдений». В первых версиях MatrixNet абсолютно точно выбирал ту ранжирующую функцию, которая давала минимальную сумму квадратов невязок, то есть использовался мнк. В настоящее время максимизируют pFound, но pFound как и сумма квадратов невязок является функцией от наблюдений.

Фундаментальные особенности методов
Квинтэссенция статьи. Которая вызывает максимум вопросов. Попытаюсь сформулировать максимально аккуратно.
У астронома может сложится обманное впечатление, что он занимается вычислением орбиты. Но на самом деле он занимается аппроксимацией, то есть вульгарной подгонкой вычислений под наблюдения. На вход в метод подаются наблюдения положений небесного тела, и на выходе получаются они же (положения), только уже вычисленные. Орбита определяется в качестве побочного эффекта. И далеко не всегда выбранная орбита, которая лучше всего аппроксимирует наблюдения, является лучшим приближением к реальной орбите небесного тела. Из чего я формулирую
Особенность №1: то, что наблюдаем, то и вычисляем
На вход MatrixNet подаются оценки пар <запрос, документ>. Эти оценки проставляют асессоры. Значит и на выходе MatrixNet мы имеем оценки пар <запрос,документ>. Только уже вычисленные.

Возражение: MatrixNet уже не минимизирует сумму квадратов невязок, а максимизирует pFound.
Ответ: но pFound как и сумма квадратов невязок является функцией от оценок пар <запрос, документ>:
Цитата (РОМИП 2009): Значениями pRel[i] в нашей модели являются оценки релевантности по запросу.
В переводе на русский: если выбранная MatrixNet функция ранжирования хорошо угадывает оценки, которые проставляют асессоры, то pFound будет максимальным. Если же функция ранжирования угадывает оценки плохо, то вперед попадут менее релевантные сайты, а значит pFound не будет максимальным. По определению самого pFound.

Отсюда можно сделать
Практический вывод №1: необходимым (не не достаточным) условием хорошего ранжирования является соответствие документа критериям максимальной асессорской оценки (Rel+ в случае коммерческих запросов)
Если сформулировать в стиле Платона Щукина, то совет будет звучать так: делайте документы (сайты) такими, чтобы асессор (а значит и MatrixNet) мог поставить им лучшую из возможных оценок.
Вторая фундаментальная особенность методов имеет более любопытное практическое применение.
При определении орбит параметры можно разделить на две группы. Одни из них вычисляются хорошо, другие не очень.
Например, наклонение орбиты, определяется очень хорошо. Если ошибка в этом параметре большая, то вычисленные значения положения небесного тела будут чем дальше, тем больше разбегаться от наблюдаемых. Астроном может наблюдать угол наклона орбиты небесного тела относительно орбиты Земли. (Этот угол хорошо видно на первом изображении в статье, хотя из-за взаимного движения Земли и Марса получается знак зорро Z aka попятное оно же ретроградное движение; обсуждаемый угол — верхняя и нижняя планки Z).
А, например, большая полуось орбиты небесного тела вычисляется не очень хорошо. Данный параметр орбиты напрямую связан с расстоянием от Земли до небесного тела (если формулировать более аккуратно, то с расстоянием от Солнца до небесного тела, но зная расстояние от Земли до Солнца мы можем легко перейти от одного расстояния к другому). Но это расстояние на короткой дуге движения наблюдать невозможно. Перехожу к формулировке:
Особенность №2.1: параметры аппроксимирующей функции (орбиты, ранжирования), которые можно явным или косвенным образом наблюдать, имеют максимальную корреляцию (оказывают максимальное влияние) с результатом вычислений (положениями, оценками)
Особенность №2.2: параметры аппроксимирующей функции (орбиты, ранжирования), которые нельзя непосредственно наблюдать, можно варьировать в максимальном диапазоне допустимых значений без оказания существенного влияния на результат

Эти утверждения лучше всего проиллюстрировать на конкретных примерах.
- Асессор может наблюдать ассортимент магазина, поэтому можно утверждать, что магазины с малым ассортиментом не могут получать максимальные оценки (Rel+) от асессоров, а следовательно MatrixNet не может научиться хорошо ранжировать такие магазины.
- Асессор не наблюдает даты создания документов, поэтому MatrixNet может ранжировать одинаково высоко старые и новые документы
- Асессор не наблюдает тИЦ домена, поэтому MatrixNet может ранжировать одинаково высоко документы с как с доменов с большим так и с малым тИЦ
- Асессор наблюдает частоту использования запроса в документе, поэтому документы с малой частотой использования будут оцениваться как малорелевантные (Rel-), но документы со сверхбольшой плотностью могут расцениваться как спамные (Spam)
Возражение: это всё ерунда, потому что машинное обучение как раз и позволяет находить не самые очевидные зависимости между оценками асессоров и параметрами документов.
Ответ: из учебника по машинному обучению: из статистической значимости параметра не следует адекватность модели.
Перевод на русский. Никто не запрещает устанавливать подобные зависимости. Весь вопрос в том, может ли алгоритм сам «отказаться» от этой зависимости, обучаясь ранжировать документы без неё или может ли инженер Яндекса принудительно обнулить эту зависимость. Без ухудшения pFound. Мой ответ: может легко. Потому что если асессор или живой посетитель не может наблюдать данной зависимости, то она и не может быть определяющей.